1.4 KiB
lec10
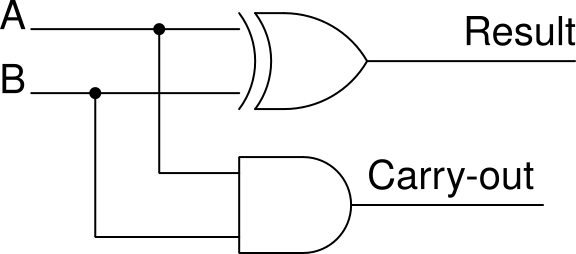
Half-adder
This will be the building block for adding bit-strings together later on however, for now we are going to just add two singular bits. To accomplish this we'll build a half adder.
This means our logic circuit must adhere to the following logic table. If both inputs are 0 then our result is 0 and we don't have to carry anything out. If only one input A/B is 1 then our result will clearly be 1 and our carry will be 0. Finally if both inputs are 0 then since we can't fit 2 in a single bit it means we have to carry-out a 1, and our result will be 0.
With all of this in mind we have a table to guide how we will implement our logic circuit. I highly suggest that you try to build a logic circuit on your own first as most of the content is best learned through practice.
| A | B | Carry-out | Result |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Full Adder
If we only want to add single-bit's then a half-adder works fine but if we want to add multiple bits say 1011 + 0010 then we need to consider that we will likely have to chain these together.
The full-adder has 1 main difference from the half-adder, it has 3 inputs, 2 main inputs and 1 input for the carry bit.
The carry bit will propagate along the operation now if we chain these together, just like real addition!