2.5 KiB
lec10
Half-adder
This will be the building block for adding bit-strings together later on however, for now we are going to just add two singular bits. To accomplish this we'll build a half adder.
This means our logic circuit must adhere to the following logic table. If both inputs are 0 then our result is 0 and we don't have to carry anything out. If only one input A/B is 1 then our result will clearly be 1 and our carry will be 0. Finally if both inputs are 0 then since we can't fit 2 in a single bit it means we have to carry-out a 1, and our result will be 0.
With all of this in mind we have a table to guide how we will implement our logic circuit. I highly suggest that you try to build a logic circuit on your own first as most of the content is best learned through practice.
| A | B | Carry-out | Result |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Full Adder
If we only want to add single-bit's then a half-adder works fine but if we want to add multiple bits say 1011 + 0010 then we need to consider that we will likely have to chain these together.
The full-adder has 1 main difference from the half-adder, it has 3 inputs, 2 main inputs and 1 input for the carry bit.
The carry bit will propagate along the operation now if we chain these together, just like real addition!
With this we can start chaining together multiple Full-adders we can start adding multiple bits at the same time since the carry now propagates along the chain.
Ripple Adders
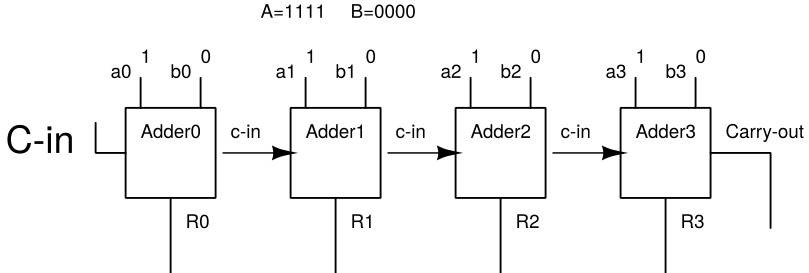
An N-bit adder is really just made up of Full adders chained together. Each adder is chained to the next by the carry-out line which then acts as the next adder's carry-in line. If we have say a 4-bit ripple adder, then each bit in the bit strings will go to a different adder. For now the initial carry in bit will be fed a 0 everytime.
Here we see that our 4-bit input A & B have the values 1111 & 0000 respectively.
The 0th bit goes to Adder0, the 1th goes to Adder1, and so on.
You should have also noticed that each one also takes a carry-in, which for now is 0 but it does mean we have to let the comutation happen one adder at a time.
None of the sequential adders can do anything if the previous have done anything yet either.
At the end of it all we get some bit results, and a carry-out.
We can then simply reassemble the results back into one bit-string to assemble our final result.