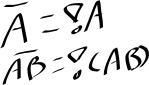2.7 KiB
lec9
This lecture has a corresponding activity found in lab/ it is called combinational-logic.md.
It is more useful to practice combinational logic as opposed to read about it so the sub section here will be minimal in information.
It's recommended that you try as many of the problems in the activity until you understand the concept, don't bother doing them all.
Combinational Logic
OR
a+b is equivalent to saying a or b.
AND
ab is equivalent to saying a and b.
Note that this syntax is simlar to multiplication so a*b is equivalent to the above.
NOT
!a is equivalent to saying not a.
We can also denote it with a bar over the expression we want to not.
Big AND
Behavior is the same as an and but instead of two inputs we can have many more inputs.
It will only ever return a 1 if all inputs are 1.
Big OR
Again we are mimicing the behvior of the normal or gate but this time we can have multiple inputs as opposed to just two. If only one of the many inputs is 1 then we return a 1 for the output of the Big OR.
Decoders
Here we'll learn by doing
Selector = 2 Bits
Output = 4 Bits
As a challenge you can try using the combinational logic gates from above to try and tackle this yourself
| s1 | s2 | o3 | o2 | o1 | o0 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
Multiplexor
Typically we'll refer to multiplexors by their size.
what does it do?
It takes a signal as 2^n inputs and out puts out n signals as output.
Example: We have a selector(s0), two inputs[in0 & in1], and one output out.
The selector will select an input and we will generate some output in out.
| s0 | i1 | i0 | out |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
This ultimately lets us pick data out of memory given some address.
Half Adder
For now we'll take two inputs and get 1 output, with a carry-output.
Let's add 2 bits
| a | b | out |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
What about the carry bit however? What would it look like given the preivous operations?
| a | b | carryout |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Before what this implies note that the result of the carryout resembles
Full Adder
Two inputs, One output, One carry-out, One carry-in
Here we'll add up a & b(inputs) and c carry-in
| c | a | b | output |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |